IPR-Modelle
Allgemein
Die Ergebnisse einer IPR-Berechnung ist die Menge, die von einer Artikelposition (SKU) bestellt werden muss (Losgröße), wie viel als Pufferbestand für den gewünschten Service (Sicherheitsbestand) vorhanden sein muss und bei welchem Bestand ein Auftrag platziert werden soll (Bestellpunkt).
Beachten Sie, dass 2 Parameter vorhanden sind: Max. Periodenbedarf und Max. Deckungszeit Sicherheitsbestand. Diese Parameter werden in der Planungshierarchie definiert und zur Begrenzung der Losgröße und des Sicherheitsbestands verwendet, sodass sie nicht übermäßig hoch werden. Diese sind besonders nützlich, wenn Sie das EOQ-Modell verwenden, da günstige Artikel in sehr hohen Mengen bestellt werden können (kann in einigen Fällen mehrere Jahre abdecken). Das gleiche gilt für den mit Service Level kontrollierten Sicherheitsbestand, wenn anormal hohe Transaktionen nicht als anomal gekennzeichnet werden, führt dies zu hohen Sicherheitsbeständen. Diese Felder 2 verhindern, dass die berechnete Verlustgröße und Sicherheitsbestände höher sind als die Anzahl der Tage, die Sie in diesen Feldern angeben. Dadurch werden diese Modell stabil und sicher.
Es gibt auch 2 Parameter, die für Bestandsartikel als Darstellung der Mindestmenge und Max. Kapazitätsmenge festgelegt werden können. Die Darstellung der Mindestmenge gibt an, wie niedrig der Sicherheitsbestand eines Artikels sein darf. Wenn das Modell einen höheren Sicherheitsbestand als die Mindestmenge ausgibt, wird der höhere Wert für den Sicherheitsbestand als Sicherheitsbestand verwendet. Die Höchstmenge Kapazität ist die maximale Anzahl der Einheiten, die nach dem Eingang der Artikel den geplanten Bestand darstellen. Das heißt: (Sicherheitsbestand + Bestellmenge) <= Höchstmenge Kapazität. Beachten Sie, dass es keine Garantie dafür gibt, dass Ihre verfügbare Menge die Höchstmenge Kapazität nicht übersteigt. Dies hängt vom Bedarf während der Vorlaufzeit ab; wenn er niedriger als erwartet ist, wird die Höchstmenge überschritten. Es ist jedoch geplant, diese nicht zu überschreiten. Es gibt ein Feld im Artikel und in der Planungshierarchie, in dem festgelegt werden kann, ob IPR bei der Berechnung der Ergebnisse die maximale Kapazitätseinstellung berücksichtigen soll oder nicht. Der Grund, ein Maximum festzulegen und sie nicht bei der Berechnung zu berücksichtigen, kann sein, dass der Empfangsstandort nur darauf hingewiesen werden soll, dass ein Artikel sein maximales Limit überschreitet, aber trotzdem die berechnete Menge des IPR gesendet werden soll.
Wenn eine Lieferroute mit dem berechneten Artikel verknüpft ist, verwendet IPR bei der Planung der Einkaufsparameter Informationen aus der Route und Vorlaufzeiten in der Lieferkettenmatrix als Artikelvorlaufzeit und Zykluszeit.
IPR kann für Artikel mit Planungsmethode B verwendet werden, für die die Modelle unten erläutert werden. IPR kann auch für Artikel mit den Planungsmethoden A, D, E, F, G und M verwendet werden, berechnet dann nur den Sicherheitsbestand und das Ergebnis wird in das Feld „Sicherheitsbestand“ des Bestandsartikels oder auf der Registerkarte „Zeitraumabhängiger Sicherheitsbestand“ unter Bestandsartikel/Planungsdaten/Allgemein (Zeitraumabhängiger Sicherheitsbestand) gespeichert. Weitere Informationen finden Sie unter IPR - Zeitraumabhängiger Sicherheitsbestand.
Um dies zu bestimmen, es gibt 4 verschiedene Modelle/Parameter, die festgelegt werden müssen
- Bedarfsmodell
- Sicherheitsbestandsmodell
- Bestellmengenmodell
- Bestellpunktmodell
Das Bedarfsmodell bestimmt, wo Sie für den zukünftigen Bedarf suchen, dieses Modell hat 3 Einstellungen:
Bedarfsmodell
Sicherheitsbestandsmodell
Losgrößenmodell
Bestellpunktmodell
- Manuell
- Vorlaufzeitgesteuert
- Lebenszyklus - Langsamdreher
- Vorlaufzeit - Langsamdreher
- Croston - Lebenszyklus
- Croston - Vorlaufzeit
Beachten Sie, dass Sie die detaillierten Berechnungen in einer Excel-Tabelle angezeigt werden können, wenn Sie Zugriff auf die IPR-Server-Webseite <http://<IPR/DP_SERVER_MACHINE_NAME>:<IPR/DP_SERVER_PORT_NUMBER>/ipr/> z. B. „http://inmino1:5010/ipr/“ haben. Geben Sie einfach die Adresse in Ihrem Webbrowser ein.
Bedarfsmodell - jährliche Prognose
Diese Einstellungen verwenden einfach das Feld für Bestandsartikel mit der Bezeichnung „Jährl. Prognose Kons. Menge” als Jahresbedarf für den Artikel. Der Jahresverbrauch kann auch manuell festgelegt werden.
Bedarfsmodell - Verlauf
Verwendet die Vorlaufzeit, Zykluszeit, Anzahl Entnahmen in der Vorlaufzeit und durchschnittliche Menge pro Entnahme zur Berechnung der jährlichen Nachfrage.
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
Wenn Sie den Bestandsartikel abrufen (Planungsdaten/Auftragspunkt), sehen Sie die Jahresergebnisse im Feld „Geschätzter Jahresbedarf”. Diese Einstellung ist einem einfachen Prognosemodell ähnlich.
Bedarfsmodell - Prognose
Der künftige Bedarf wird von der Prognose aus Bedarfsplanung abgerufen. Die Prognose wird aus der Prognose in festgelegten Intervallen (je nach Modelle) ausgelesen.
Sicherheitsbestand - Manuell
Verwendet den manuell festgesetzten Sicherheitsbestand im Feld Sicherheitsbestand im Bestandsartikel.
Sicherheitsbestand - Deckung
Wenn die Deckungszeit für den Sicherheitsbestand auf der Basis der Deckungszeit Sicherheitsbestand und des Bedarfsmodells festgelegt wird. Der Sicherheitsbestand sollte die Anzahl der durch die beiden bestimmten Tagesbedarfe abdecken. Wenn Sie beispielsweise eine jährliche Prognose als Bedarfsmodell mit einem Jahresbedarf von 876 und 25 als Deckungszeit Sicherheitsbestand haben, führt dies zu einem Sicherheitsbestand von (876/365*25) 60.
Wenn die Prognose als Bedarfsmodell ausgewählt ist. Der Sicherheitsbestand wird anhand der Prognose im Intervall unten berechnet
Sicherheitsbestand - Historische Unsicherheit
Die historische Unsicherheit verwendet die gemessene Standardabweichung zur Berechnung des Sicherheitsbestands mithilfe des Servicegrads. Der Servicegrad ist der Bedarf, den Sie für ein Service Level im Lebenszyklus des Artikels haben, die Standardableitung gibt die Abweichung des Bedarfs während der Vorlaufzeit an. Die Standardableitung wird vom Hintergrundjob Analyse der Bestandsabweichung in IFS berechnet.
Die Standardableitung in der Vorlaufzeit wird anhand der historischen Beobachtungen aus dem Job Analyse der Bedarfsabweichung gemessen. Der erste Schritt bei der Suche nach der entsprechenden Sicherheitsfaktor für einen beliebigen gegebenen Service-Prozentsatz ist der Wert zur Berechnung der Service-Funktion f(k).
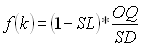
| OQ | Bestellmenge (Losgröße) |
| SD | Standardableitung |
| SL | Servicebedarf (0 - 0.999999) |
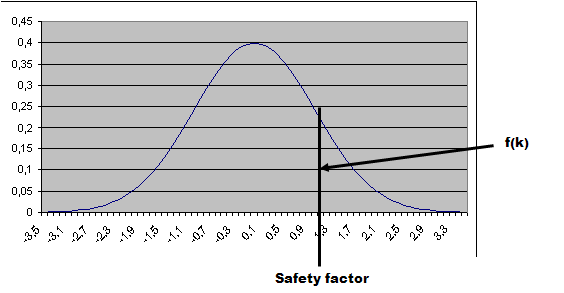
Beachten Sie, dass die Losgröße umso mehr ansteigt, desto kleiner der Sicherheitsbestand wird. Dieselbe Ertrags-ID verringert die Standardableitung.
Sie können die folgende Tabelle zum bestimmen des richtigen Sicherheitsfaktors für eine bestimmte Servicefunktion verwenden.
| Sicherheitsfaktor | Servicefunktion |
| 0,00 | 0,3989 |
| 0,60 | 0,1687 |
| 1,20 | 0,0561 |
| 1,80 | 0,0143 |
| 2,40 | 0,0027 |
| 3,00 | 0,0004 |
Abschließend wir der Sicherheitsbestand berechnet:
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
| SD | Standardableitung |
| SS | Sicherheitsbestand |
Beachten Sie, dass die Standardableitung geändert wird, wenn das dynamische Deckungsmodell verwendet wird, siehe Dynamische Deckung.
Sicherheitsbestand - mittlerer absoluter Fehler
Diese Methode ist eine ähnliche Funktion wie die Historische Unbestimmtheit mit dem wichtigen Unterschied, dass die Standardableitung innerhalb der Vorlaufzeit von der Prognose in der Bedarfsplanung abgerufen wird und zusammen mit den Servicegrad zur Berechnung des Sicherheitsbestands verwendet wird. Der Servicegrad ist der Bedarf, den Sie für ein Service Level im Lebenszyklus des Artikels haben, die Standardableitung gibt die Abweichung des Bedarfs während der Vorlaufzeit an. Die Standardableitung wird vom MSE-Fehler für die Vorlaufzeit (plus eventueller Zykluszeit) aus der Bedarfsplanung berechnet. Die Berechnung erfolgt eine Vorlaufzeit in die Zukunft (siehe Abbildung).
Die Standardableitung in der Vorlaufzeit wird anhand der historischen Beobachtungen aus dem Job Analyse der Bedarfsabweichung gemessen. Der erste Schritt bei der Suche nach der entsprechenden Sicherheitsfaktor für einen beliebigen gegebenen Service-Prozentsatz ist der Wert zur Berechnung der Service-Funktion f(k).
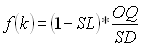
| OQ | Bestellmenge (Losgröße) |
| SD | Standardableitung |
| SL | Servicebedarf (0 - 0.999999) |
Beachten Sie, dass die Losgröße umso mehr ansteigt, desto kleiner der Sicherheitsbestand wird. Dieselbe Ertrags-ID verringert die Standardableitung.
Sie können die folgende Tabelle zum bestimmen des richtigen Sicherheitsfaktors für eine bestimmte Servicefunktion verwenden.
| Sicherheitsfaktor | Servicefunktion |
| 0,00 | 0,3989 |
| 0,60 | 0,1687 |
| 1,20 | 0,0561 |
| 1,80 | 0,0143 |
| 2,40 | 0,0027 |
| 3,00 | 0,0004 |
Abschließend wir der Sicherheitsbestand berechnet:
<![if!msEquation]>
<![if !vml]><![endif]><![endif]>
| SD | Standardableitung |
| SS | Sicherheitsbestand |
Beachten Sie, dass die Standardableitung geändert wird, wenn das dynamische Deckungsmodell verwendet wird, siehe Dynamische Deckung.
Losgrößenmodell - manuell
Die Losgröße wird manuell für den Bestandsartikel festgelegt.
Losgrößenmodell - Deckungszeit
Wenn die Deckungszeit für den Sicherheitsbestand auf der Basis der Deckungszeit/Losgröße und des Bedarfsmodells festgelegt wird. Die Losgröße sollte die Anzahl der durch die beiden bestimmten Tagesbedarfe abdecken. Wenn Sie beispielsweise eine jährliche Prognose als Bedarfsmodell mit einem Jahresbedarf von 365 und 15 als Deckungszeit/Losgröße haben, führt dies zu einer Losgröße von (365/365*15) 15. Wenn Deckung verwendet wird und Bedarfsmodell auf Prognose eingestellt ist. Die Losgröße wird auf die Deckung der prognostizierten Menge von der Vorlaufzeit in die Zukunft für die Anzahl der Tage der Deckungszeit/Losgröße eingestellt.
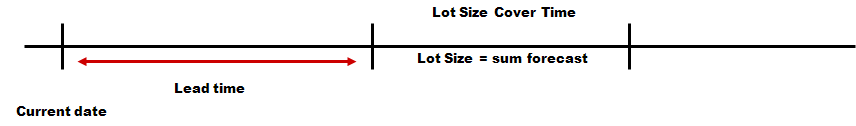
Losgrößenmodell - EOQ (wirtschaftliche Losgröße)
Die EOQ gleicht die Bestellkosten mit den Lagerkosten der Waren aus und berechnet die Losgröße so, dass die Summe dieser Kosten minimiert wird.
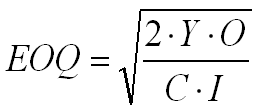
| Y | Erwarteter Jahresbedarf |
| D | Erste Periode mit historischem Bedarf |
| O | Bestellkosten |
| C | Kostenpreis |
| I | Lagerrabatt |
Bei Auswahl von Prognose als Bedarfsmodell verwenden wir eine besondere Variante mit dem EOQ-Modell, das saisonale Änderungen und Trends der Prognose berücksichtigt, bei der Berechnung der Losgröße.
Algorithmus
1. Mithilfe des prognostizierten Jahresbedarfs Y_0 EOQ_1, beginnend mit dem Ende der Vorlaufzeit berechnen
2. Ermittlung, wie lange T_1 EOQ_1 läuft ab am Ende der Vorlaufzeit.
3. Berechnet den prognostizierten Bedarf im Bereich T_1, und sucht den erwarteten Jahresbedarf Y_1 durch Extrapolation
4. Eine neue EOQ_(n+1) mit Y_1 als jährliche Nachfrage berechnen.
Bei einer Wiederholung ab Punkt 2 wird dies 3 mal ausgeführt, die resultierende EOQ_4 ist die endgültige EOQ.
Dynamische Abdeckung
Bei der dynamischen Abdeckung handelt es sich um ein Losgrößenmodell, das Informationen zur Routen-ID verwendet. Der Punkt bei diesem Modell ist, dass Sie an jedem Tag, an dem der Artikel nach der mit dem Artikel verknüpften Routen-ID geliefert werden soll, eine Lieferung von Artikeln erhalten. Anhand der Routen-ID berechnet IPR den spätesten Auftragstag und den entsprechenden Liefertag für jeden Liefertag in der Routen-ID. Die berechnete Losgröße muss so sein, dass die Bestandsmenge am Liefertag des nächsten Auftrags dem Sicherheitsbestand entspricht. Kurz gesagt, wenn der Verkauf wie geplant verläuft, erhalten Sie jedes Mal, wenn der Artikel gemäß der Routen-ID-Info geliefert werden kann, eine Lieferung.
Die Routeninfo bedeutet in der Regel, dass die Vorlaufzeit und die Zykluszeit je nach Wochentag variieren, da die Standardableitung usw. durch den Job „Bedarfsableitung des Bestandsartikels analysieren“ im Modul IFS Materialwirtschaft berechnet wird, der die erwartete Vorlaufzeit und Zykluszeit des Artikels verwendet. Die gemessenen Standardableitungen werden daher mit dieser Formel geändert, bevor sie zur Berechnung des Sicherheitsbestands verwendet werden.
<![if!msEquation]> <![if !vml]>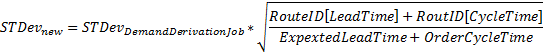
<![endif]><![endif]>
Die Losgröße wird wie folgt berechnet:
<![if !vml]> <![endif]> |
Auftragsdatum n |
<![if !vml]> <![endif]> |
Eingangs-/Lieferdatum n |
| SS | Sicherheitsbest. |
| MENGE | Lagerbestand |
| PS | Geplante Lieferung (On..Rn +1) |
<![if!msEquation]> <![if !vml]>
<![endif]><![endif]>
Bestellpunktmodell - Manuell
Der Bestellpunkt wird manuell für den Bestandsartikel festgelegt.
Bestellpunktmodell - Vorlaufzeitgesteuert
Wenn der über die Vorlaufzeit gesteuerte Bestellpunkt verwendet wird, wird der Bestellpunkt anhand des berechneten Sicherheitsbestand plus den erwarteten Bedarf während der Vorlaufzeit + der möglichen Zykluszeit berechnet. Der Bedarf, der verwendet wird, wird durch das Bedarfsmodell festgelegt. Wenn Sicherheitsbestand 10 ist, die Vorlaufzeit 10 ist und das Bedarfsmodell eine jährliche Prognose von 730 ausgibt.
Der Bestellpunkt ist 10 + (10*2) = 30
Bestellpunktmodell - Lebenszyklus Langsamdreher
Wenn der Bestellpunkt für Langsamdreher verwendet wird, wird der Bestellpunkt gemäß der Poisson-Verteilung festgelegt. HINWEIS: Beachten Sie, dass der Sicherheitsbestand in diesem Modell nicht verwendet wird. In diesem Modell wird der Bestellpunkt direkt berechnet. Der Unterschied zwischen Vorlaufzeit und Lebenszyklus ist, dass bei der Verwendung des Lebenszyklus der Servicegrad für den gesamten Lebenszyklus auch Füllrate genannt wird. Wenn die für den Servicegrad festgelegt Vorlaufzeit nur für die Vorlaufzeitperiode oder 1 Servicebedarf gilt, ist sie die niedrigste Wahrscheinlichkeit eines Fehlbestands in einem Auftragszyklus ist.
| OQ | Bestellmenge (Losgröße) |
| SD | Standardableitung |
| SL | Servicebedarf (0 - 0.999999) |
| R | Bestellpunkt/Wiederbestellstufe |
| DL | Zufälliger Bedarf während der Vorlaufzeit |
| λ | Bedarfsrate (Tagesbedarf) |
Der Bestellpunkt wird dann von folgenden Algorithmen berechnet.
Schritt 1 fortfahren. (Begrenzende Einleitung)) k = 0
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
Schritt 2 (begrenzende Prüfung) Wenn F(k) > SL legen Sie R1=k fest und fahren Sie mit Schritt 4 andernfalls Schritt 3 fort
Schritt 3 (begrenzendes Inkrement) k = k + 1
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
und mit Schritt 2 fortfahren.
Schritt 4 Wenn OQ = 1 Stop R1 ist der Wiederbestellpunkt. Andernfalls weiter mit Schritt 5.
Schritt 5 (Interation für OQ) Bestimmung: Rq = R1-OQ
<![if!msEquation]>
<![if !vml]>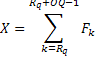
<![endif]><![endif]>
Schritt 6 (Entscheidung vergrößern / verkleinern) Wenn X < SL * OQ fahren Sie mit Schritt 7a (Steigerung von Rq bis X > SL = * OQ ansonsten weiter mit Schritt 8a (Rq weiter verringern bis X<SL*OQ
Schritt 7a (Anstieg für Zielerreichung)
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
Schritt 7b (Prüfung) Wenn X > SL * OQ, ist Rq der gewünschte Wiederbestellpunkt. Andernfalls weiter mit Schritt 7a
Schritt 8a Rq (absteigend zum Erreichen des Ziels) = Rq-1
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
Schritt 8b (Prüfung) Wenn X > SL * OQ, ist Rq+1 der gewünschte Wiederbestellpunkt. Andernfalls weiter mit Schritt 8a. In der oben genannten Schritte werden 8a und 8b verwendet, falls die theoretisch niedrigere Grenze für Rq fehlschlägt (bei kleinen OQ möglich)
Bestellpunktmodell - Vorlaufzeit Langsamdreher
Wenn der Bestellpunkt für Langsamdreher verwendet wird, wird der Bestellpunkt gemäß der Poisson-Verteilung festgelegt. HINWEIS: Beachten Sie, dass der Sicherheitsbestand in diesem Modell nicht verwendet wird. In diesem Modell wird der Bestellpunkt direkt berechnet. Der Unterschied zwischen Vorlaufzeit und Lebenszyklus ist, dass bei der Verwendung des Lebenszyklus der Servicegrad für den gesamten Lebenszyklus auch Füllrate genannt wird. Wenn die für den Servicegrad festgelegt Vorlaufzeit nur für die Vorlaufzeitperiode oder 1 Servicebedarf gilt, ist sie die niedrigste Wahrscheinlichkeit eines Fehlbestands in einem Auftragszyklus ist.
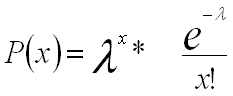
| X | Anzahl Vorkommnisse |
| I | Die historischen Häufigkeit in Vorlaufzeit |
Die Poisson-Verteilung gibt die Wahrscheinlichkeit für 0, 1, 2, 3, 4 an. Bedarfsvorkommnisse in der Vorlaufzeit. Es wird angenommen, dass die Vorkommnisse unabhängig sind. Zum Abrufen des Bestellpunkts multiplizieren Sie die richtige Anzahl Bedarfsvorkommnisse mit dem Durchschnittsbedarf pro Vorkommnis.
<![if !vml]>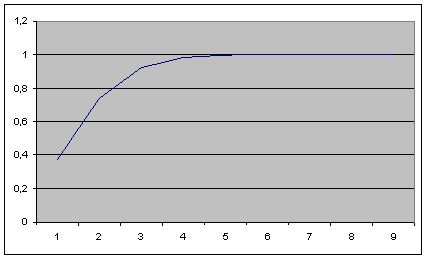
<![endif]>
| Häufigkeit | Cul. Prob |
| 0 | 0,3678 |
| 1 | 0,7357 |
| 2 | 0,9196 |
| 3 | 0,981 |
| 4 | 0,9963 |
| 5 | 0,994 |
| 6 | 0,9999 |
Häufigkeit λ = 1 Durchschnittliche Entnahmemenge = 2
In diesem Beispiel ist der Servicebedarf auf 90 % gesetzt, woraus sich ein Bestellpunkt von 4 (2*2) ergibt. Dies ergibt einen theoretischen Service während der Vorlaufzeit von 91,96 %.
Bestellpunktmodell - Croston-Lebenszyklus
Dies ist dasselbe wir das Lebenszyklusmodell für Langsamdreher, jedoch wird die Häufigkeit aus dem Croston-Prognosemodell anstatt aus direkten Messungen der Häufigkeit und Bedarfsgrößen aus historischen Absätzen ausgelesen.
Diese Nummern werden mit der Länge der Periode, die als die Periodenversion der Bedarfsplanung ausgewählt ist, ausgedrückt. Damit diese Option Sinn macht, muss die Periodenversion fast identische Periodenlängen (Wochen, Monate, Quartale oder andere einheitliche Perioden) aufweisen. Also wenn der Artikel, die Vorlaufzeit und die Periode, die Länge in der Bedarfsplanung nicht ähnlich ist sollten keine Croston-Langsamdrehermodell verwendet werden.
Angenommen, dass die Vorlaufzeit kleiner als die geplante Periode ist, und eine Zeitverschiebung durchgeführt wird, um das geschätzte Intervall zwischen Bedarfen während der Vorlaufzeit (t2) zu erhalten, kann dies so berechnet werden.
| z | Bedarfsgröße bei Bedarf, aus dem Croston-Modell in der Bedarfsplanung (Bedarfsgröße) |
| q | Das Intervall zwischen Bedarfsereignissen aus dem Corston-Modell in der Bedarfsplanung (Intervall zwischen Bedarfen |
| t1 | Durchschnittliche Dauer der Periode in der Bedarfsplanung |
| t2 | Vorlaufzeit des Artikels |
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
<![if !msEquation]><![endif]>
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
Die Bedarfsgröße kann während der Vorlaufzeit t2 geschätzt werden, dies kann wie folgt berechnet werden
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
<![if !msEquation]><![endif]>
<![if!msEquation]>
<![if !vml]>
<![endif]><![endif]>
<![if !msEquation]>Dann werden diese im selben Algorithmus wie für Langsamdreher Lebenszyklus verwendet.<![endif]>
Bestellpunktmodell - Croston-Vorlaufzeit
Dies ist dasselbe wie das Lebenszyklusmodell für Langsamdreher, jedoch wird die Häufigkeit aus dem Croston-Prognosemodell anstatt aus direkten Messungen der Häufigkeit und Bedarfsgrößen aus historischen Absätzen ausgelesen.
Diese Nummern werden mit der Länge der Periode, die als die Periodenversion der Bedarfsplanung ausgewählt ist, ausgedrückt. Damit diese Option Sinn macht, muss die Periodenversion fast identische Periodenlängen (Wochen, Monate, Quartale oder andere einheitliche Perioden) aufweisen. Also wenn der Artikel, die Vorlaufzeit und die Periode, die Länge in der Bedarfsplanung nicht ähnlich ist sollten keine Croston-Langsamdrehermodell verwendet werden.
Angenommen, dass die Vorlaufzeit kleiner als die geplante Periode ist, und eine Zeitverschiebung durchgeführt wird, um das geschätzte Intervall zwischen Bedarfen während der Vorlaufzeit (t2) zu erhalten, kann dies so berechnet werden.
| z | Bedarfsgröße bei Bedarf, aus dem Croston-Modell in der Bedarfsplanung (Bedarfsgröße) |
| q | Das Intervall zwischen Bedarfsereignissen aus dem Corston-Modell in der Bedarfsplanung (Intervall zwischen Bedarfen |
| t1 | Durchschnittliche Dauer der Periode in der Bedarfsplanung |
| t2 | Vorlaufzeit des Artikels |
<![if!msEquation]>
<![if !vml]><![endif]><![endif]>
<![if !msEquation]><![endif]>
<![if!msEquation]>
<![if !vml]><![endif]><![endif]>
Die Bedarfsgröße kann während der Vorlaufzeit t2 geschätzt werden, dies kann wie folgt berechnet werden
<![if!msEquation]>
<![if !vml]><![endif]><![endif]>
<![if !msEquation]><![endif]>
<![if!msEquation]>
<![if !vml]><![endif]><![endif]>
Die 1/q2 werden jetzt als I in der Poisson-Verteilung verwendet. z2 wird als erwarteter Bedarf verwendet, wenn ein Vorkommnis eintritt.
<![if !msEquation]><![endif]>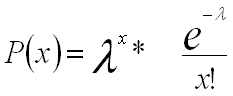<![if !msEquation]><![endif]>
<![if !msEquation]><![endif]> Die Poisson-Verteilung gibt die Wahrscheinlichkeit für 0, 1, 2, 3, 4 an. Bedarfsvorkommnisse in der Vorlaufzeit. Es wird angenommen, dass die Vorkommnisse unabhängig sind. Zum Abrufen des Bestellpunkts multiplizieren Sie die richtige Anzahl Bedarfsvorkommnisse mit dem Durchschnittsbedarf pro Vorkommnis (z2).<![if !msEquation]><![endif]>